Amplitude modulation: Difference between revisions
No edit summary |
(Wikification. Fix crappy English. Please put thoughts about the article's development on the talk page.) |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
'''Amplitude modulation''' ('''AM''') is a [[modulation scheme]], notably used in AM radio. |
|||
== What is AM? == |
|||
| ⚫ | |||
[[Modulation Scheme]], have been widely used in Analog Radio.used by e.g. by analog radio. |
|||
| ⚫ | |||
An Amplitude Modulator modulates the Amplitude of an sinoid Carrier signal using the incoming signal. |
|||
Base for transmission is a sinusoid carrier signal with continuous carrier frequency <math>f_c</math>: |
|||
: <math>\omega_c := 2 \pi f_c</math> |
|||
This is modulated by the incoming signal, here modeled by a simple sine with frequency <math>f_m</math>: |
|||
| ⚫ | |||
: <math>\omega_m := 2 \pi f_m</math> |
|||
The actual signal coming out of the AM modulator is simply the product of both functions <math>\omega_c \cdot \omega_m</math>. Evaluating this in detail leads to the expression: |
|||
: <math>u_{AM}(t) = U_c \cdot cos(\omega_c \ t) \cdot [1 + m \cdot cos(\omega_m \ t)]</math> |
|||
where <math>U_c</math> is the modulation amplitude and <math>m</math> the modulation index. |
|||
| ⚫ | |||
[[ |
[[File:AM mathematical desc.jpg|Description]] |
||
The first formula |
The first formula describes what happens in time domain. It's basically multiplying of two cosine signals leading to the time domain picture in the example below. |
||
The second formula describes the frequency response, the frequency spectrum consists of three spectrum lines at each time t. The first term is the carrier, for |
The second formula describes the frequency response, the frequency spectrum consists of three spectrum lines at each time, t. The first term is the carrier, for sure the carrier is in the spectrum, the second and third terms describe two spectrum lines around the carrier, and their amplitude is dependent on the modulation index, m. As the modulating signal varies the lines around the carrier frequency are varying. |
||
''we should add an frequeny response picture below in the example'' |
|||
| ⚫ | |||
| ⚫ | |||
{| |
{| |
||
|[[ |
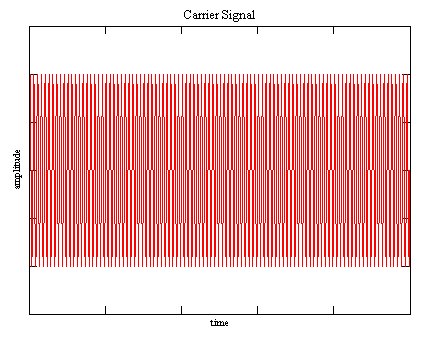
| [[File:AM picture1.jpg|frame|Carrier signal in time domain]] |
||
|[[ |
| [[File:AM picture4.jpg|frame|Carrier signal in frequency domain (to be added)]] |
||
|- |
|- |
||
|[[ |
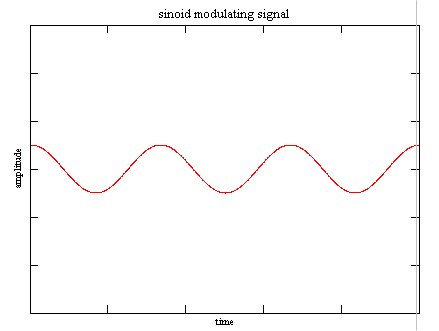
| [[File:AM picture2.jpg|frame|Modulating signal in time domain]] |
||
|[[ |
| [[File:AM picture5.jpg|frame|Modulating signal in frequency domain (to be added)]] |
||
|- |
|- |
||
|[[ |
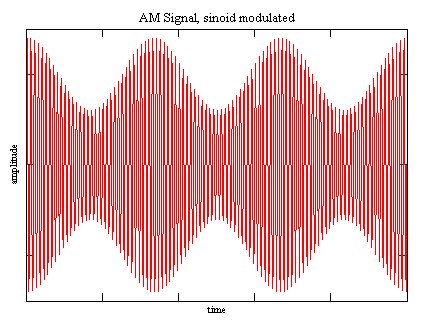
| [[File:AM picture3.jpg|frame|AM signal]] |
||
|[[ |
| [[File:AM picture6.jpg|frame|AM signal in frequency domain (to be added)]] |
||
|} |
|} |
||
== Special kinds == |
|||
* Double sideband suppressed carrier (DSSC) |
|||
* Single side band (SSB) |
|||
| ⚫ | |||
* [[Quadrature Amplitude Modulation]] (QAM) (used in digital TV applications) |
|||
== |
== Acquired bandwidth == |
||
| ⚫ | |||
*DSSC, Double Sideband Supressed Carrier |
|||
*SSB, Single Side Band |
|||
| ⚫ | |||
*[[Quadrature_Amplitude_Modulation|QAM, Quadrature Amplitude Modulation]] |
|||
== Aquired Bandwidth == |
|||
| ⚫ | |||
''it would be nice to have a picture showing how AM signals in the frequency spectrum behave and how much bandwidth they allocate. A short overview of AM-related problems would be nice, too. Has anybody of you this info handy?'' |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
== |
== External links == |
||
| ⚫ | |||
* [[Wikipedia:History of radio|History of radio]] at Wikipedia |
|||
[[Category:Technology]] |
|||
| ⚫ | |||
Latest revision as of 07:21, 26 December 2016
Amplitude modulation (AM) is a modulation scheme, notably used in AM radio.
An amplitude transceiver modulates the amplitude of an sinusoid carrier signal using the incoming signal. The carrier signal is sinusoid with a fixed Frequency, usually much higher than the highest frequency occurring in the spectrum of the modulating signal.
Mathematical setting
Base for transmission is a sinusoid carrier signal with continuous carrier frequency <math>f_c</math>:
- <math>\omega_c := 2 \pi f_c</math>
This is modulated by the incoming signal, here modeled by a simple sine with frequency <math>f_m</math>:
- <math>\omega_m := 2 \pi f_m</math>
The actual signal coming out of the AM modulator is simply the product of both functions <math>\omega_c \cdot \omega_m</math>. Evaluating this in detail leads to the expression:
- <math>u_{AM}(t) = U_c \cdot cos(\omega_c \ t) \cdot [1 + m \cdot cos(\omega_m \ t)]</math>
where <math>U_c</math> is the modulation amplitude and <math>m</math> the modulation index.
The first formula describes what happens in time domain. It's basically multiplying of two cosine signals leading to the time domain picture in the example below.
The second formula describes the frequency response, the frequency spectrum consists of three spectrum lines at each time, t. The first term is the carrier, for sure the carrier is in the spectrum, the second and third terms describe two spectrum lines around the carrier, and their amplitude is dependent on the modulation index, m. As the modulating signal varies the lines around the carrier frequency are varying.
Example
File:AM picture4.jpg Carrier signal in frequency domain (to be added) | |
File:AM picture5.jpg Modulating signal in frequency domain (to be added) | |
File:AM picture6.jpg AM signal in frequency domain (to be added) |
Special kinds
- Double sideband suppressed carrier (DSSC)
- Single side band (SSB)
- Vestigial side band modulation (VSB) (used in digital TV applications)
- Quadrature Amplitude Modulation (QAM) (used in digital TV applications)
Acquired bandwidth
An AM signal shows up as a single peak in the frequency spectrum.
Noise sensitivity
Echoes, multipath signaling, atmospheric and meteorologic phenomenons like lightings and electrostatic discharges contribute noise that simply gets added to the transmitted signal. Most other Modulation Schemes are less sensitive to noise.
External links
- Wikipedia:Amplitude modulation at Wikipedia
- History of radio at Wikipedia